ortotipografía en matemáticas
Con el propósito de adecuar el estilo editorial del Centro a los estándares de la escritura en matemáticas, se retoma el siguiente texto, de la Wikilengua.
Los símbolos matemáticos no son abreviaciones, sino entidades escritas con valor completo y autónomo. No quedan por tanto sujetos a normativas de carácter lingüístico o gramatical, sino que siguen su propia lógica del lenguaje formal matemático para combinarse en expresiones y fórmulas según ciertas reglas establecidas, ya sea por tradición, ya sea por convenios internacionales, nacionales, locales o personales. Por ello, este artículo se limita a unas normas mínimas sobre notación matemática. Aunque los números en cifras son también una notación matemática, se tratan en un artículo específico.
Nombres de teorías, teoremas, constantes...
En minúscula, incluyendo métodos, reglas...:
- el quinto postulado de Euclides, el axioma de completitud, el teorema de Pitágoras
- el método de exhaución, la regla de Cramer, el problema de Dirichlet
También los conceptos se escriben con minúsculas (salvo nombres propios):
- el espacio de Hilbert, la ecuación diferencial parcial, el álgebra de Lie
- la transformada de Laplace, el grupo de Galois, la cinta de Moebius, los cuadrados mágicos
- las coordenadas cartesianas, la geometría riemanniana, el espacio métrico
- la función z de Riemann, el número transfinito, el valor propio
- la hipérbola, el concoide de Nicomedes, la distribución normal
Símbolos unarios
Son aquellos que no establecen una relación u operación entre dos entidades, sino que únicamente afectan al número, a la expresión o al símbolo que le sigue. Normalmente solo se emplean los siguientes:
- − para las cantidades negativas: −5 °C
- + para dejar claro que la cantidad es positiva: +12
- ± para indicar que la cantidad puede ser positiva o negativa ±7
- ~ para las cantidades aproximadas: ~35 kg m
- > para expresar mayor que: >21
- < para expresar menor que: <21
Todos estos símbolos unarios van unidos a la cantidad, aunque modernamente hay cada vez más tendencia a que los de desigualdad vayan con un espacio.
Signo más
El signo + usado como símbolo significa más e indica suma o un número positivo. Informalmente, se está empleando como abreviación de más de y o más, que no es su valor matemático propio. Así, no es raro ver que «+18» o «18+» se emplean con un sentido aproximado de más de 18. La forma antepuesta («+18») tiene el inconveniente de que se puede confundir con el sentido de positividad, lo que no ocurre con «18+». En textos técnicos, los símbolos adecuados para un límite inferior son > y ≥.
Símbolos binarios
Establecen una relación u operación entre dos entidades matemáticas. Entre ellas están:
- Las operaciones aritméticas: a + b, a − b, a/b, a · b, a × b
- Las igualdades, desigualdades, etc.: a = b, a < b, a > b, a ≈ b
Tienen un espacio fino antes y después, con excepción de la barra de división: a/b y cuando van en índices: xa+b.
Escalas
Es simplemente un caso especial de : como operación aritmética. En las escalas marcadas con dos puntos, al igual que en las proporciones, se deja un espacio antes y otro después del signo de división, según se refleja en las normas ISO 80000 y 5455. Es frecuente omitir los espacios de separación de millares, pero en cualquier caso también se sigue la norma general de no separar los grupos de tres cifras con puntos:
- ✓ 1 : 250 000
- ✘ 1:250.000
Símbolos literales
Los símbolos del tipo cos (coseno), tanh (tangente hiperbólica), mcd (máximo común divisor), ln (logaritmo neperiano), se escriben sin puntos ni espacios, incluso cuando se han formado a partir de varias palabras. Se escriben en redonda y muchos de ellos van en minúscula, aunque no todos, como Re e Im (partes real e imaginaria de un número complejo) o Si (seno integral).
Las funciones trigonométricas se escriben completas cuando forman parte de un planteamiento o una instrucción, pero no cuando están acompañadas por valores asociados.
- seno, coseno
- cos α + cos β = 2 cos 1(α + β) cos 1(α - β)
Cuando a una función trigonométrica le sigue un paréntesis, entonces se escribe sin espacio.
- ✓ sen(cos α + cos β)
- ✘ sen (cos α + cos β)
Cursiva y redonda
La siguiente imagen resume de modo esquemático las pautas más importantes:
Por constante se entiende la que tiene un valor numérico universal y se obtiene por teoremas matemáticos. Las constantes físicas, cuyo valor numérico depende del sistema de unidades y, a menudo, se determinan experimentalmente, van en cursiva. La escritura de las constantes matemáticas en redonda es lo recomendado en la norma ISO 80000, pero sigue siendo muy frecuente la regla tradicional de escribirlas en cursiva.
Paréntesis
Mientras que en el texto se sigue el orden de anidamiento ([{}]), en álgebra y aritmética elemental se sigue el opuesto: {[()]}. Fuera de la aritmética, suelen tener sentidos especiales que hay que conservar. Así, una función siempre emplea (), como f(x), y no otros signos. Para conjuntos suele ser {} y para operadores es frecuente []. Cuando se anidan y es importante conservar el valor establecido, no se cambian los signos, sino que se va incrementando ligeramente su tamaño:
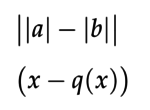
Estas convenciones se respetan incluso en el texto, por lo que f(x) dentro de un inciso con paréntesis conserva esta forma:
Símbolos complejos
Los símbolos matemáticos de variables, funciones, magnitudes, etc., pueden tener subíndices, exponentes y distintos tipos de acentos gráficos con diversas funciones. En esto se diferencian de las unidades físicas, que no pueden ir modificadas más que por exponentes.
Así, â o í pueden ser un determinado operador (o el operador que corresponde a una magnitud); ρéter puede ser la densidad del éter, etc. La grafía de estos elementos es la que corresponde a cada uno de ellos por separado, de modo que en el último ejemplo ρ va en cursiva y «éter» va en redonda; en v², el símbolo de la velocidad va en cursiva, pero el número 2 va en redonda.

